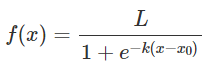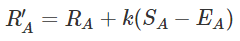연속된 메모리 공간에 할당되고 모두 동일한 타입으로 사용된다.
void func(int arr[]); // sizeof(arr) : 8
// void func(int* arr);
int main() {
int arr[] = { 1, 2, 3, 4, 5 }; // sizeof(arr) : 20
func(arr);
return 0;
}배열을 함수의 인수로 넘겨주면 주소값이 전달되기 때문에 포인터의 크기가 나온다.
인수가 배열이라는 것을 명시적으로 알려줄 뿐 사실은 포인터와 완전히 동일하다.
◾ 배열의 요소를 뒤집을 때 투 포인터를 사용하면 시간 복잡도는 O(N/2), 공간 복잡도는 그대로이다.
부분 배열
◾ 배열의 크기가 N이라면 부분 배열들의 개수는 N^3에 근접한다.
◾ 3중 for문을 사용하면 배열의 부분 배열들을 출력할 수 있다. (i=0<n, j=0<n, k=i<=j)
부분 배열의 합 : 브루트 포스
int largestSubarraySum(int arr[], int n) {
int largestSum = 0;
for (int i = 0; i < n; ++i) {
for (int j = i; j < n; ++j) {
int subarraySum = 0;
for (int k = i; k <= j; ++k) {
subarraySum += arr[k];
}
largestSum = max(largestSum, subarraySum);
}
}
return largestSum;
}완전 탐색에 의해 계산되고 공간 복잡도는 O(1), 시간 복잡도는 O(N^3)이다.
반복문을 두개로 줄일 수 있으므로 O(N^2)까지 낮출 수 있다.
부분 배열의 합 : 누적합
int largestSubarraySum(int arr[], int n) {
vector<int> prefix(n, 0);
prefix[0] = arr[0];
for (int = 1; i < n; ++i)
prefix[i] = prefix[i-1] + arr[i];
int largestSum = 0;
for (int i = 0; i < n; ++i) {
for (int j = i; j < n; ++j) {
int subarraySub = i > 0 ? prefix[j] - prefix[i-1] : prefix[j];
largestSum = max(largestSum, subarraySum);
}
}
return largestSum;
}공간 복잡도는 O(N), 시간 복잡도는 O(N+N^2) = O(N^2)이다.
부분 배열의 합 : Kadane 알고리즘
int largestSubarraySum(int arr[], int n) {
int currentSum = arr[0];
int largestSum = arr[0];
for (int i = 1; i < n; ++i) {
currentSum = max(currentSum + arr[i], arr[i]);
largestSum = max(largestSum, currentSum);
}
return largestSum;
}현재 누적합과 최대 누적합을 별도로 관리하여 선형으로 계산해나간다.
공간 복잡도는 O(1), 시간 복잡도는 O(N)이다.
'이론 > 자료구조&알고리즘' 카테고리의 다른 글
| Vector Data Structure (0) | 2023.02.08 |
|---|---|
| Pointers & Dynamic Memory (0) | 2023.02.07 |
| 2D Arrays (0) | 2023.02.07 |
| Character Arrays/Strings (0) | 2023.02.03 |
| Basic Sorting Algorithms (0) | 2023.02.03 |