101. 데이터 들여다보기
보통 게임의 데이터는 원시 상태라서 바로 읽기에는 무리가 있다. 이를 읽기 쉽게 만들기 위해 사용되는 보편적인 방법은 도수분포표를 만드는 것이다.
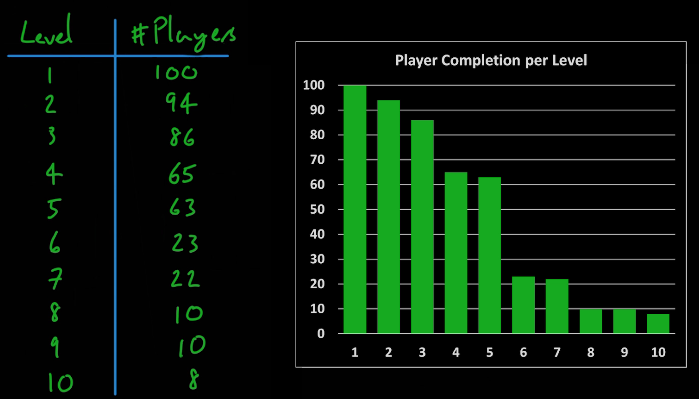
차트를 그림으로써 시각적으로 5단계와 6단계 사이에 무언가 문제가 있다는 사실을 추측할 수 있게 된다.
다만 어떤 문제인지는 구체적으로 확인할 수 없고 추정만 가능하다. 이 때 추가적으로 버그리포트나 플레이어 피드백 등을 확인하여 문제점을 구체화 시켜야 한다.
막대차트 대신 상황에 맞춰서 파이차트도 그릴 수 있다. 한가지 권장사항으로 차트 툴에서 제공하는 3D 차트는 피하는것이 좋다.
102. 백분율
40의 100%는 40이고 100의 40% 역시 40이다. 이를 이용하여 백분율 암산을 더 쉽게 할 수 있다.
수식으로 정리하면 x% of y = y% of x이다. 25의 24%를 구하는 것보다 24의 25%를 구하는게 훨씬 쉽다.

예시 하나를 들어보자. 어떤 플레이어가 랭크게임을 시작하기 전의 레이팅이 1123이었고 끝난후의 레이팅이 1251이면 11.3%가 증가한 것이다.
103. 시그마 표기법

반복문을 작성하는 것과 같다. 시그마는 그저 모든 요소를 더할 뿐이다.
104. 평균
평균에는 산술평균, 중앙값, 최빈값 총 3가지가 존재한다.
◾ 산술평균 : 우리가 아는 그 평균.
장점 : 연속적인 수치자료에 사용될 수 있다 (예: 킬 평균)
단점 : 수치자료가 아닐 때 사용할 수 없다. (예: 유저들의 선호무기)
극단치가 있을 때 값이 왜곡된다. (예: 99명의 0킬과 1명의 1000킬 산술평균은 10킬)
◾ 중앙값 : 데이터 셋의 가운데 값. 원소의 개수가 짝수인 경우 가운데를 기준으로 좌우값의 산술평균값을 산출한다.
장점 : 극단치와 관계가 없어진다.
단점 : 정렬이 되지 않으면 사용이 불가능하다. 마찬가지로 수치자료에만 사용이 가능하다.
◾ 최빈값 : 데이터 셋에서 가장 많이 나타난 값.
105. 극단치
어떤 데이터를 다루던 간에 극단치는 존재할 수 있다.

위와 같은 산포도에서 극단치가 존재하는 경우 우리는 세 가지 선택을 할 수 있다.
첫번째, 그냥 무시하는 것이다. 극단치도 데이터의 일부이기 때문이다. 다만 해당 수치를 무시할 뿐이다.
두번째, 데이터 셋에서 제외시킨다. 너무 눈에 띄는 극단치라면 제외하고 싶기 때문이다.
세번째, 어떤 기준에 의해 데이터를 반영하여 원래 되어야 했을 값을 추정하여 값을 조정한다.
세가지 방법중 상황에 따라 필요한것을 선택하면 된다.
보통 데이터의 무결성을 위해 극단치까지 포함된 보고서와 극단치를 처리한 보고서 총 2개를 작성하는게 일반적이다.
'이론 > 게임수학' 카테고리의 다른 글
| [게임수학] 확률과 통계 (3) (0) | 2023.01.16 |
|---|---|
| [게임수학] 확률과 통계 (2) (0) | 2023.01.16 |
| [게임수학] 회전과 보간 (4) (0) | 2023.01.13 |
| [게임수학] 회전과 보간 (3) (0) | 2023.01.13 |
| [게임수학] 회전과 보간 (2) (0) | 2023.01.12 |
