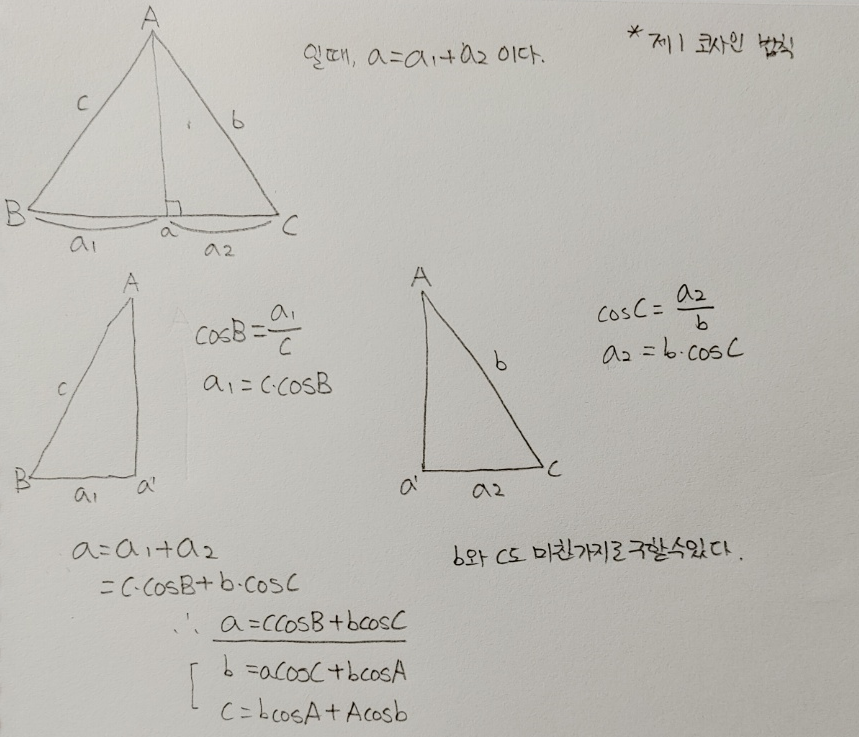
[게임수학]

- 2차원 평면에서 (x,y) 를 90˚ 만큼 회전시키면 (-y,x)이고, -90˚ 회전시키면 (y,-x) 이다.

복소 평면에서 임의의 복소수 (a,b)에 단위 복소수 (0,1)를 곱하면 (-b,a)가 된다. 즉, 90˚ 회전이 이루어진다.

- 사영 공간의 좌표를 클립 좌표라고 부른다

- 삼각형 클리핑 : 월드공간의 좌표를 사용하지 않고 투영행렬을 적용한 후의 좌표를 사용

단위원에서의 sin, cos 함수의 특징으로 삼각함수의 덧셈정리를 유도하고 그를 이용하여 행렬을 만들어낸다.

참고 링크

https://youtu.be/K2V_caa1QY0

https://youtu.be/1VKuI6OgHq8

https://youtu.be/DkRd2OtctRU

더보기

 

더보기

 

내적

3차원 벡터 A=(ax, ay, az), B=(bx, by, bz)가 주어졌을 때,

A·B = (axbx + ayby + azbz) = |A||B|cosθ 로 계산할 수 있으며 결과는 스칼라값으로 나온다.

|A||B|cosθ는 제2코사인법칙을 사용하면 구할 수 있는 동일한 식이다.

교환법칙, 분배법칙, 스칼라곱에 대한 결합법칙이 성립한다.

더보기

 

■ 두 벡터간의 직교성을 판별하는데 사용할 수 있다.

A·B=0 이라면 두 벡터는 직교(90°)한다.

A·B=1 이라면 두 벡터는 평행(0°)한다. 같은 방향을 바라본다는 뜻이다.

A·B=-1 이라면 두 벡터는 평행(180°)한다. 서로 다른 방향을 바라본다는 뜻이다.

앞뒤판별에 사용할 수 있다.

■ 두 벡터간의 투영 길이를 구하는데 사용할 수 있다.

외적

외적은 3차원 벡터에 대해서만 사용할 수 있다.

3차원 벡터 3차원 벡터 A=(ax, ay, az), B=(bx, by, bz)가 주어졌을 때,

A×B = (aybz-azby, azbx-axbz, axby-aybx) 로 계산할 수 있다.

교환법칙과 결합법칙이 성립하지 않는다. (교환하는 경우 부호가 반대로 나온다.)

벡터 삼중곱

A×(B×C) = (A·C)·B - (A·B)·C (사원수 식 유도에서 사용됨)

더보기

두 벡터를 외적하면 두 벡터에 모두 직교하는 새로운 벡터가 생성된다.

어떤 오브젝트 Obj가 있을때,

크기 변환 행렬 (S)

회전 변환 행렬 (R)

이동 변환 행렬 (T)

--> 연산의 순서가 중요함. 크기->회전->이동 순서로 계산해야 한다. 행벡터 기준인 경우 수식은 M = T·R·S로 작성한다.

각각의 행렬에 역행렬을 곱하면 본래의 상태로 돌아간다. 위의 계산순서의 반대로 계산한다. M⁻¹ = S⁻¹·R⁻¹·T⁻¹

M은 로컬공간의 좌표를 월드좌표로 바꿔주는 합성 행렬이다.

M·Obj = 오브젝트의 최종 월드 좌표

뷰 행렬 (V)

--> 카메라에 트랜스폼이 적용된 경우, 이동 행렬의 역행렬을 이용하여 구한다.

월드좌표 기준이었던 것이 카메라를 기준으로 변한다. 카메라에 렌더링 하려면 V·M를 계산한다.

렌더링 과정에 사용한다.

V·M·Obj = 오브젝트의 뷰 좌표

원근 투영 행렬 (P)

--> 원근감을 추가하기 위해 NDC 좌표계에 대응하여 미리 계산해둔 행렬.

행렬의 장점을 살리기 위해 마지막 결과값에 z축의 역수를 곱해준다. 행렬 성분의 공통분모이기 때문.

렌더링 과정에 사용한다.

P·V·M·Obj = 오브젝트를 원근투영한 클립 좌표