87. 극좌표
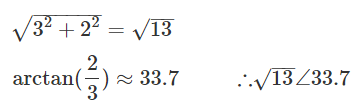
직교형식으로 된 복소수 a가 3+2i라고 했을때 극형식으로 바꾸면 √13∠33.7이 나오게 된다.

극형식으로 표현된 √13∠33.7을 단위원의 삼각함수에서 유도된 공식에 극형식의 값을 대입하면 다시 직교형식으로 바꿀 수 있다.
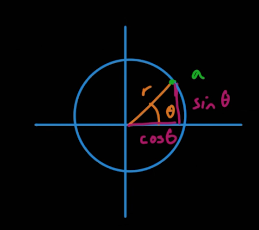

복소수의 곱셈 결과는 두 복소수의 크기를 곱한것과 두 복소수의 각을 더한것과 같다고 했었다.
이를 이용하여 일반식으로 정리할 수 있다.
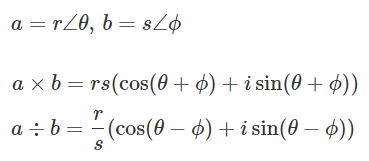
일반적으로 덧셈과 뺄셈은 직교형식으로 동류항끼리 계산하는게 더 쉽지만 곱셈과 나눗셈은 극형식으로 계산하는게 훨씬 쉽다.
그래서 두가지 방식을 다 알아야한다.
88. 회전 행렬

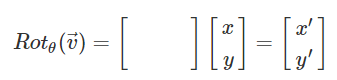
2차원 벡터 v=(x, y)를 θ만큼 회전시킨 결과가 v'=(x', y')라고 했을 때, 행렬로 표현하면 위와 같을 것이다.
열벡터에 곱해서 회전이 이루어지는 행렬을 찾는것이 이번 목표이다.
우선은 2x2 단위행렬을 떠올리자. 여기서부터 회전 행렬을 만들어 나갈 것이다.
단위행렬은 열벡터 2개로 나누어서 생각할 수 있다.
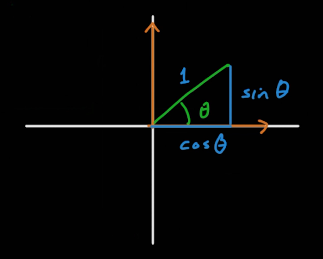
이 단위행렬에 의해 만들어진 벡터(1,0)로 원을 그리면 단위원이 될 것이고 θ만큼 회전시키면 인접변은 cosθ, 대변은 sinθ가 된다.

열벡터 한쪽이 채워졌다.
이번에는 다른 열벡터(0,1)를 θ만큼 회전시킬 차례이다.

두 벡터 모두 크기가 1이기때문에 길이 역시 똑같을 것이다. 하지만 sinθ가 2사분면으로 넘어왔기 때문에 음수가 된다.

단위행렬로 시작해서 회전행렬을 모두 구했다.

점 하나에 대한 회전이기 때문에 여러 정점으로 이루어진 오브젝트라면 각 정점마다 연산을 해야한다.
89. 오일러 행렬
2차원에서의 회전 행렬을 알아봤으니 이제는 3차원에서의 회전 행렬을 알아볼 차례이다.
마찬가지로 3x3 단위행렬에서 시작한다. 그리고 각 축을 기준으로 회전시킨다.
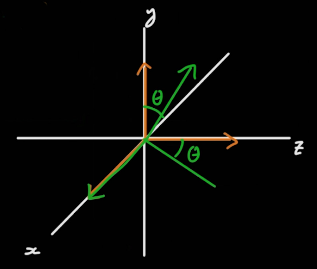
x축을 기준으로 (1,0,0)을 아무리 회전시켜봐야 그대로이고 나머지 축은 θ만큼 시계방향으로 회전하게 된다.
기준 축으로는 값의 변화가 없기때문에 사실상 2개의 축, 즉 2차원에서의 회전이라고 보면 되기 때문에 나머지 축에 대해서는 2차원에서의 회전을 적용하면 된다.

그렇게 구해진 각 축별 회전행렬은 위와 같다.

보통 피치-롤-요 순으로 연산한다.
그런데 이런 오일러각 회전에는 짐벌락이라는 아주 중대한 문제가 존재한다.
90. 짐벌락

중간축에 의해 외부와 내부 2개의 축이 일치하게 되면 축 하나가 상실된다.
자주 사용하는 축을 기준으로 연산 순서를 바꿔서 짐벌락 발생을 최소화시킬수 있지만 짐벌락을 막는것은 불가능하다.
'이론 > 게임수학' 카테고리의 다른 글
| [게임수학] 회전과 보간 (4) (0) | 2023.01.13 |
|---|---|
| [게임수학] 회전과 보간 (3) (0) | 2023.01.13 |
| [게임수학] 회전과 보간 (1) (0) | 2023.01.12 |
| [게임수학] 벡터와 행렬 (4) (0) | 2023.01.11 |
| [게임수학] 벡터와 행렬 (3) (0) | 2023.01.11 |
