106. 왜도
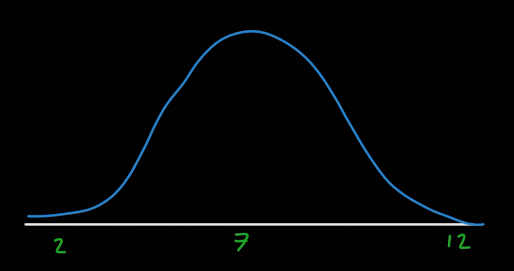
정규분포는 확률과 통계에서 많이 사용된다.
정규분포에서 최고점은 최빈값에 해당되지만, 대칭적인 정규분포에서는 산술평균, 중앙값, 최빈값 모두에 해당된다.
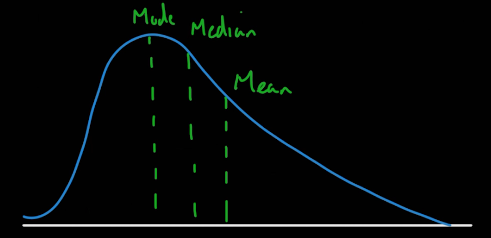
정규분포가 양의 왜도를 가지면 산술 평균과 중앙값은 최빈값보다 커진다. 반대로 음의 왜도를 가지면 최빈값보다 작아진다.
107. 사분위간 범위
양 끝에 존재하는 극단치는 스팬을 크게 만든다. 실제로 관심 있는 데이터는 극단치를 제외한 가운데 부분이기 때문에 사분위간 범위라는것을 사용한다.
말이 어려운것 같지만 전체 범위를 4등분한 사이에 있는 값들의 범위이다. (1/2)

Q1~Q3 사이의 값들이 사분위수 범위이다.
108. 표준편차
먼저 분산을 알아야한다. 분산은 산술평균을 구해서 각 데이터와 산술평균과의 차이를 제곱하여 다시 산술평균을 내는 것이다.
이렇게 구한 분산의 제곱근이 표준편차가 된다. 산술평균값에 표준편차값을 ±하여 만들어진 범위안에 대부분의 값들이 위치하게 된다.

단, 주의해야할점이 하나 있다. 모든 데이터를 포함하는 모집단인지, 혹은 일부 데이터만 포함된 표본집단인지 여부에 따라 n의 값이 달라진다.
모집단인 경우 위의 공식 그대로 쓰고 표본집단인 경우에는 n-1을 사용한다. 그 이유는 오차범위를 넓힘으로써 표본에서 잃어버렸을수도 있는 데이터를 고려해주기 위함이다.
또한 표본집단의 표준편차는 σ가 아닌 s로 표기한다.
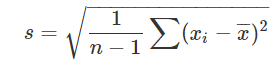
계산은 똑같은데 표기만 달라질뿐이다. 조금 번거롭다고 생각될지 모르지만 기호만 보고도 어떤 표준편차인지 알 수 있다.
109. 상관
상관은 데이터간에 관계가 있는지 여부를 알 수 있다.
상관여부를 시각적으로 확인할 수 있는 가장 쉬운 방법
1. 가능한 많은 점이 지나도록 선분을 긋는다.
2. 선의 위쪽과 아래쪽에 거의 같은 수의 점이 있도록 한다.
3. 점들이 선으로부터 멀리 떨어지지 않아야 한다.

상관관계를 표현하는 상관계수를 r이라고 한다. -1과 1사이의 값을 가질 수 있고 -1이면 완벽한 음의 상관관계, 1이면 완벽한 양의 상관관계, 0이면 아무런 상관이 없다.
r을 구하는 방법은 모집단의 산술평균을 먼저 구하고 같은 행의 두 값을 곱한 뒤에 산술평균을 낸다. (공분산)
이 공분산을 x의 표준편차와 y의 표준편차를 곱한 값으로 나눠주면 r을 구할 수 있다.

보통 0.7보다 큰 값이면 큰 양의 상관관계, 0.5~0.7이면 중간정도의 양의 상관관계, 0.3~0.5는 약한 양의 상관관계, 0~0.3은 상관관계가 없다고 본다.
111. 데이터 정규화

어떤 데이터셋 x가 주어졌을 때, 해당 데이터셋의 최소값과 최대값, 그리고 단일 데이터들이 필요하다.
각 단일 데이터마다 위의 연산을 수행하면 0~1사이의 정규화된 값으로 조정된다. 만약 0~1이 아닌 다른 범위가 필요하다면 해당 결과에 (범위 최대값 - 범위 최소값)을 곱해준 뒤에 범위 최소값을 더해주면 된다.

'이론 > 게임수학' 카테고리의 다른 글
| [게임수학] 확률과 통계 (4) (0) | 2023.01.17 |
|---|---|
| [게임수학] 확률과 통계 (3) (0) | 2023.01.16 |
| [게임수학] 확률과 통계 (1) (0) | 2023.01.14 |
| [게임수학] 회전과 보간 (4) (0) | 2023.01.13 |
| [게임수학] 회전과 보간 (3) (0) | 2023.01.13 |
