112. 확률의 기초
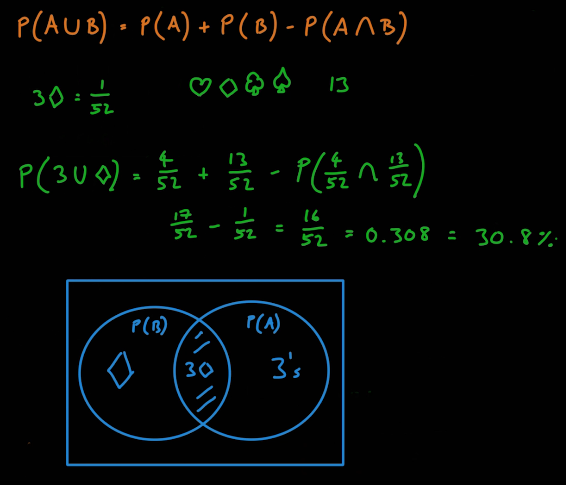
교집합을 빼는 이유는 겹치는 부분이 두번 더해졌기 때문이다.
113. 연속 시행

독립사건의 연속시행은 기존의 결과가 이후의 결과에 영향을 주지 않기때문에 두 확률을 곱하면 구할 수 있다.
예를 들면 주사위를 두번 던져서 6을 연속으로 뽑을 확률이다.
종속사건의 연속시행은 기존의 결과가 이후의 결과에 영향을 주기 때문에 수형도를 그려서 각각의 경우를 맞는 조건에 따라 계산해야한다.
예를 들면 카드 두장을 뽑아서 에이스를 연속으로 뽑거나 두장 중 에이스를 한번이라도 뽑을 확률이다.

수형도의 모든 확률을 더하면 반드시 1이 나온다. 만약 1이 나오지 않았다면 잘못 작성한것이다.
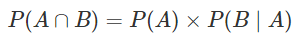
B는 A에 종속되어있기 때문에 독립시행일때와 식이 다르다.
114. 여사건 법칙
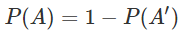
위의 종속사건의 연속시행을 계산하는 경우라면 사실 모든 확률을 더하는것보다 해당되지 않는 경우를 빼는것이 더 쉽고 빠르게 구할 수 있다. 모든 경우는 아니고 이게 더 쉬운 경우가 있다는 것이다. 또한 종속사건의 연속시행 뿐만 아니라 독립사건의 연속시행에도 당연히 적용할 수 있다.
예를 들면 동전을 6번 던져서 최소 한번 이상 앞면이 나올 확률이다. 총 64가지의 경우의 수가 생기는데 이를 수형도를 통해 모든 확률을 더하기보다는 앞면이 한번도 안나오는 경우의 수는 딱 한가지이기 때문에 1에서 이 확률만 빼주면 된다.
확률을 구하기 어려운것 같으면 반대로 뒤집어서 생각해보아야 한다.
115. 이론적 확률과 경험적 확률
시행 횟수(표본의 집단)가 많을수록 이론적 확률에 근접하게된다. 큰 수의 법칙이다.
확률을 이론적으로 구할 수 있지만 따로 경험적 확률이 있어야 하는 이유는 뭘까? 바로 검증때문이다.
확률을 코드로 작성하다보면 실수 또는 예상치 못한 부분에서 변수가 발생하여 의도치 않은 결과가 나올 수도 있다.
또는 애니팡같은 게임들은 가능한 조합과 무작위성을 추측하여 이론적 확률을 계산하기 매우 어렵기때문에 매우 많은 시뮬레이션을 통해 직접 데이터를 확인하는 경우가 있다.
'이론 > 게임수학' 카테고리의 다른 글
| [게임수학] 확률과 통계 (4) (0) | 2023.01.17 |
|---|---|
| [게임수학] 확률과 통계 (2) (0) | 2023.01.16 |
| [게임수학] 확률과 통계 (1) (0) | 2023.01.14 |
| [게임수학] 회전과 보간 (4) (0) | 2023.01.13 |
| [게임수학] 회전과 보간 (3) (0) | 2023.01.13 |
