116. 평균값 정리
도박사의 오류(평균의 오류)라는 것이 있다.
동전을 연속으로 6번 던졌을 때, 5번 연속 앞면이 나온다면 다음 시행시 확률상 뒷면이 나올거라 기대하는 것이다.
하지만 완전한 독립시행이라서 언제나 50%이다.
큰 수의 법칙을 떠올리며 시행횟수가 많아질수록 점점 평균에 근접할거라고 착각하는 것이다. 하지만 이는 다르게 생각하면 균형을 맞추기 위해 뒷면이 나올 확률이 증가해야 한다는 결론에 도달하게 된다.
완전한 독립시행에서 종속시행이라는 결론을 도출하는 것인데 이는 말도 안되는 오류이다.
이성적으로 보면 말도 안되지만 그런 확률을 겪은 플레이어가 오류에 빠지지 않게 할 수는 없다. 왜냐면 확률이 안정적인 평균으로 수렴할만큼의 수많은 시행횟수를 시도하는 플레이어는 거의 없다고 봐도 무방하기 때문이다. 게다가 거기까지 도달하기 위해 겪는 부정적인 경험을 무시할 수 없다.
그래서 큰 수의 법칙에 의해 확률이 수렴하기 전의 확률 변동을 받아들이게 하기 위해서는 완전한 독립시행이 아닌 종속시행으로 어느정도 보정하는 경우도 있다. (ex:강화실패 시 확률 상승)
확률보정을 유저가 느끼지 못하게 뒤에서 조절할수도 있고 강화시도처럼 직접 확인할수 있게 제공할수도 있으므로 상황에 맞게 선택하여 사용하면 된다.
117. 베이즈의 정리
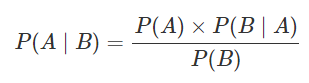
확률 이론에서 가장 중요한 식이다.
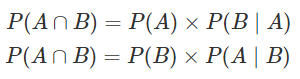
여기에서 유도된 식이다. P(B)로 나누면 베이즈의 정리가 된다.
베이즈의 정리는 조건부 확률을 구하는 한 가지 방법이다.
정말 유명한 문제로 베이즈의 정리를 증명해보자.

아무런 선택을 하지 않았을 때 상품을 얻을 확률은 P(1)=P(2)=P(3)=1/3 으로 동일하다.
하지만 문을 고르고 사회자가 꽝인 문을 연 뒤에 선택을 바꿨을 때, 확률이 변동하게 된다.
참가자가 1번 문을 고른 상태에서 사회자가 2번 문을 열 확률을 b라고 해보자.

참가자는 언제나 1번문을 열고, 사회자는 절대 상품이 들어있는 문을 열 수 없으므로 확률은 위와 같다.

P(A|b) : b문을 열었을 때, A문에 경품이 있을 확률
P(A) : A문에 경품이 있을 확률
P(b|A) : A문에 경품이 있을 때, 진행자가 B문을 선택할 확률
식에 대입하며 계산하면 1/3이 나온다. 진행자가 문을 열든 말든 내가 처음 골랐을 때의 확률은 그대로이다.
하지만 선택을 바꾸면 남은 확률이 합산되기 때문에 2/3으로 변동한다. 사회자가 정보를 알고 정답문을 절대 열지 않는다는것이 핵심이다.
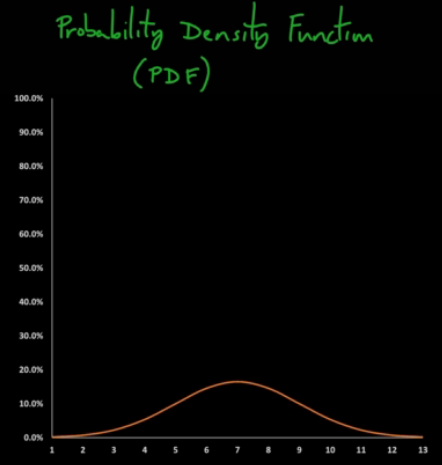
118. 누적분포함수
119. 엘로(ELO) 평점 시스템
두 유저간 등급 점수의 차이가 있으면 누가 이겼는지에 따라 점수의 증감량이 다르다.
전통적인 ELO 시스템은 로지스틱 함수를 사용하여 계산한다.
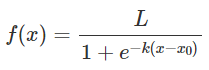
L : 곡선의 최댓값
k : 증가율
x0 : 그래프의 중앙점

Ra, Rb : A, B 플레이어의 현재 평점
10, 400과 같은 상수는 일종의 매직 넘버이다. 상대방보다 평점이 400점 높다면 승률이 10배 높다는 의미이다.
800점 높으면 100배 높아진다.
400은 임의의 수이기 때문에 게임의 상황에 맞게 변경해도 된다.

Sa : 승/무/패별로 얻는 점수 (0~1)
Ea : 플레이어가 이길 확률
k : 최대 점수 상수
승률을 구했으면 경기 결과에 따라 가중치를 두어 점수의 가감이 이루어진다.
이길 확률이 낮은 플레이어가 이기게 되면 Sa-Ea는 1에 가깝기 때문에 많은 점수를 얻고 반대로 이길 확률이 높은 플레이어가 지게되면 -1에 가깝기 때문에 많은 점수를 잃는다.
보통 k는 32로 두는편이다. 물론 임의의 수로 설정해도 무관하다. 증감되는 수의 최대치일 뿐이다.
평점 산정 시스템이 필요한 경우 ELO 평점 시스템으로 시작하는게 단순해서 이해와 구현이 쉽다.
하지만 리터럴 상수에 의존하기 때문에 상수값을 잘 설정해야 한다는 단점이 있다.
또한 기본적으로 1:1 상황에서만 동작이 가능하므로 ELO 평점 시스템은 맞지 않고 플레이어들의 실력이 같은 분포 곡선을 그리고 있어야한다는 가정이 있어야하지만 실제로는 편차가 존재하기 때문에 정규화 등의 과정을 거쳐서 수정하여 적용해야 한다.
'이론 > 게임수학' 카테고리의 다른 글
| [게임수학] 확률과 통계 (3) (0) | 2023.01.16 |
|---|---|
| [게임수학] 확률과 통계 (2) (0) | 2023.01.16 |
| [게임수학] 확률과 통계 (1) (0) | 2023.01.14 |
| [게임수학] 회전과 보간 (4) (0) | 2023.01.13 |
| [게임수학] 회전과 보간 (3) (0) | 2023.01.13 |
