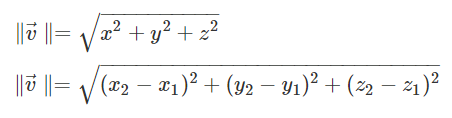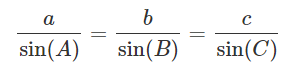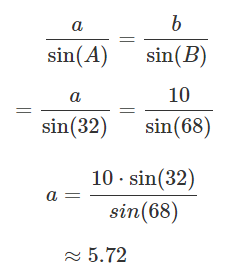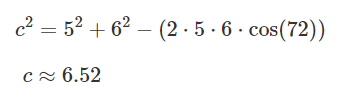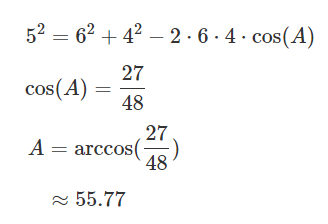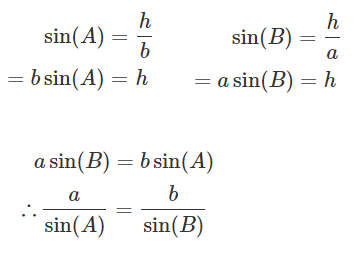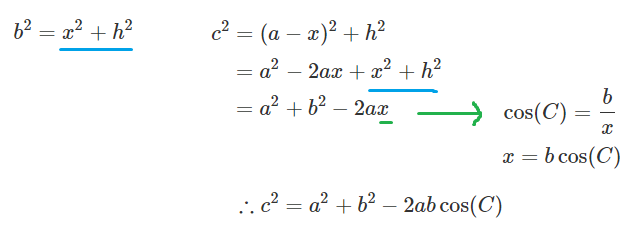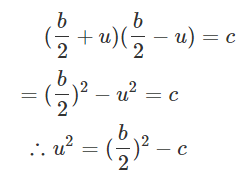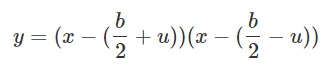70. 내적

내적의 결과는 스칼라값이다. 그래서 스칼라곱이라고도 부른다.

단위벡터를 기준으로,

◾ 두 벡터가 서로 평행하면 결과값은 1이다.

◾ 두 벡터가 서로 직교하면 결과값은 0이다.

◾ 두 벡터의 방향이 반대라면 결과값은 -1이다.

두 벡터의 직교를 기준으로 예각이면 양수, 둔각이면 음수가 된다.

내적을 사용할 수 있는 대표적인 예시로써 적이 플레이어의 앞이나 뒤에 있는지 여부를 판단하거나 적과 플레이어의 방향벡터를 내적하여 서로 마주보고있는지 또는 같은방향(뒤통수)을 보고 있는지를 판단할 수 있다.

즉, 시야판별 또는 백/헤드 어택에 사용할 수 있다는 얘기이다.

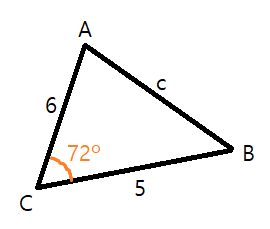
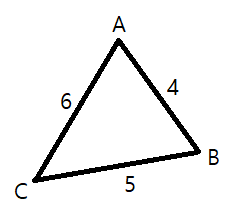
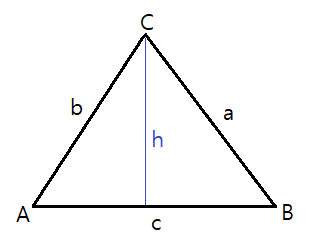
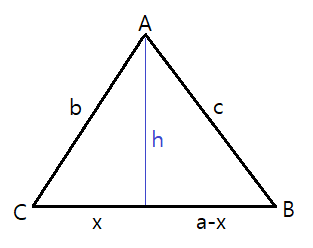
근데 이 모양이 코사인 법칙과 매우 닮아있다. 벡터의 크기는 선분의 길이와 동일하므로 치환해서 풀어보면 아래와 같은 식을 유도할 수 있다.

위에서 적은 예시 말고도 셰이더에서 빛이 어떻게 반사되는지 계산하거나 길찾기에서 너무 높은 경사를 지나가지 않도록 조절하는데 사용된다.

내적은 두 벡터끼리 비교하거나 두 벡터 사이의 각도를 재고싶을 때 사용할 수 있다.

71. 외적

외적의 결과는 두 벡터에 직교하는 법선벡터이다. 그래서 벡터곱이라고도 부른다.

내적과 달리 3차원 공간에서만 성립하고 교환법칙이 성립되지 않는다.

또한 외적의 결과로 나온 벡터의 크기는 평행사변형의 넓이와 동일하다.

두 벡터의 각도가 0º 또는 180º라면 영역을 정의할 수 없기 때문에 외적의 결과는 영벡터가 된다.

내적과 비슷하게 각도와 관련되어 있기 때문에 유도해낼 수 있는 식이 존재한다.

외적은 내적과 함께 사용되어 충돌을 감지하거나 물체를 튕기게 하는데 사용된다. 외부 표면을 계산하는데 이용되기도 한다.

72. 반사

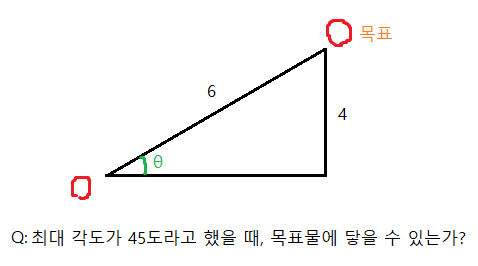
어떤 물체가 45º 각도로 벽에 충돌하게 되면 -45º 각도로 튕겨져 나와야 할 것이다. 이 때 반사의 기준은 법선 벡터가 된다.

위와 같은 상황은 벽에 부딪혀서 반사하게되면 y축과 z축은 그대로 유지되고 x축만 벽에 가로막혀서 부호가 반대로 바뀌게 게 될 것이다.

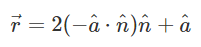
먼저 벽의 정규화된 법선벡터 n을 외적으로 구하고 이후 내적과 스칼라 연산을 통해 반사벡터 r을 구하게 된다.

식과 결과 모두 정규벡터이기 때문에 본래의 속력을 곱해주거나 가속, 감속에 따른 추가 연산을 수행해주면 된다.

73. 평면으로의 사영

우선 어디에 쓰이는지 예시부터 들고 가자.

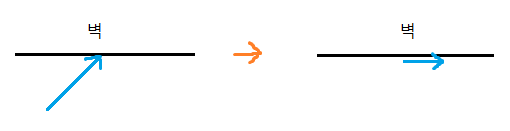
보통 레이싱 게임에서 차량이 벽에 비스듬히 부딪혔을 때, 그 즉시 멈추는게 아니라 위처럼 벽을 타고 이동하게 된다. 또는 rpg등의 게임에서 캐릭터가 벽에 붙은채로 비스듬하게 전진하면 느린 속도로 벽을 타고 이동한다.

이런것들은 이동 벡터를 평면에 사영시킴으로써 구현할 수 있다.

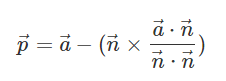
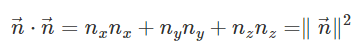
법선벡터 n이 자기자신을 내적하는것은 n의 크기의 제곱과 동일하다.

만약 n이 정규화 되어있다면 분모는 언제나 1이기 때문에 계산이 조금 더 단순해진다.

사영벡터는 법선벡터와 직교하게된다.

63. 벡터 읽고 쓰기

크기와 방향을 가지고 있다. 크기가 1인 경우 단위 벡터이다.

64. 크기와 크기의 제곱

원점에서 시작하는 벡터 OA의 크기는 직각삼각형의 빗변으로도 볼수 있기 때문에 피타고라스의 정리로 구할 수 있다.

원점에서 시작하지 않는 벡터는 직선의 방정식에서 기울기를 구하던 것처럼 변화량으로 계산하면 된다.

3차원 벡터의 크기 계산은 별 다를것 없이 z축만 추가해주면 된다.

다만 유의해야 할 점은 제곱근 연산은 비용이 꽤 큰 연산이기 때문에 크기를 구할때마다 매번 제곱근을 계산하기에는 부담스럽다. 그래서 대신 크기에 제곱을 취해서 제곱근 연산을 피한다.

어떤 값(ex:적의 공격범위)과 비교해야 할 때, 양변에 제곱을 취해서 비교하는것이 연산량이 훨씬 적다.

두 벡터 사이의 거리를 계산해야 할 때는 제곱근 연산을 피하는게 좋고 유저에게 정보를 보여줘야 할때는 정확한 정보가 필요하기 때문에 제곱근 연산을 할 수밖에 없을 것이다.

대부분의 게임 엔진은 벡터의 크기를 반환하는 함수를 위의 두 종류로 제공한다.

66. 벡터의 덧셈

활용 예)

◾ 플레이어와 카메라 간의 위치 차이 측정

◾ 바람에 밀리는 오브젝트

교환 법칙이 성립된다.

67. 스칼라 곱셈

각 요소에 스칼라값을 곱해주면 된다.

68. 벡터의 정규화

벡터의 크기가 0이라면 오류가 발생하기 때문에 주의해야한다.

69. 영벡터

프로그래밍을 하다보면 영벡터를 꽤 자주 만나게 되고 유용하게 사용하는 경우가 있다.

직전에도 언급했듯이 영벡터의 정규화를 시도하는 것에 주의해야한다.

54. 사인 법칙

위와 같은 삼각형이 주어졌을 때,

위의 식이 성립한다.

예시 문제를 하나 풀어보자.

각 2개와 변 1개를 알고 있고 변이 두 각 사이에 있지 않을 때, 나머지 값들을 구할 수 있다. (AAS)

B가 포탑이고 최대사거리가 7이라고 했을 때, 5.72 <= 7이므로 공격이 가능하다.

반대로 각 1개와 변 2개(밑변 제외)를 알고 있어도 값을 구할 수 있다. (SSA)

sin(B)가 아닌 B를 구하는게 목적이기 때문에 0.384에 역함수를 취해서 B의 값을 구한다.

단, 주의할점이 있다. 각도에 대한 사인 값만 알고 다른 정보가 없을 경우 1사분면과 2사분면의 사인값은 둘다 양수이기 때문에 해가 2개이다. (22.58º 또는 157.42º)

밑변의 길이가 다른 삼각형이 여러개 존재할 수 있는 것이다.

55. 코사인 법칙

AAS, SSA의 경우는 사인 법칙으로 구할 수 있지만 SAS(변,각,변), SSS(변3개)는 코사인 법칙으로 구할 수 있다.

이런 경우가 주어졌다면 위의 식에 그대로 대입해서 구하면 된다.

이번에는 변의 길이만 주어진 경우를 보자.

A를 구하는 경우에는 cos(A)에 역함수를 취해주면 된다.

나머지 두 각은 B에대해 한번 더 같은 과정을 수행하고 180-A-B로 간단히 구할 수 있다.

56. 사인, 코사인 법칙에 대한 설명

■ 사인 법칙 유도과정

C도 마찬가지로 A에서 수선의 발을 내려서 구하면 된다.

예각 삼각형이 아닌 둔각 삼각형이라면 삼각형 외부에 또 다른 삼각형을 그려서 직각 삼각형을 만든 다음 구하게 된다.

■ 코사인 법칙 유도과정 : https://erikanes.tistory.com/147

조금 더 단순하게 구하기

a, b 역시 동일하게 수선의 발을 내려서 직각삼각형을 만들고 식을 만들면 된다.

57. 삼각형 문제의 해법

◾ 각도만 3개 주어졌을 때(AAA) : 각 변의 길이를 구할 수 없다.

◾ 직각 삼각형이고 빗변을 구해야 하는 경우(SSS) : 피타고라스의 정리 이용

◾ 직각 삼각형이고 빗변이 아닌 변을 구해야 하는 경우 : SOH, CAH, TOA

◾ AAS, SSA, ASA : 사인 법칙 이용. 답이 2개일수도 있으니 주의해야한다

◾ SAS, SSS : 코사인 법칙 이용

59. 사인파의 조작

◾ 진폭(amplitude) : 사인 파동의 높낮이를 조절한다.

◾ 주파수(frequency) : 사인 파동의 간격을 조절한다.

60. 파장의 합성

* 추후 사진 첨부 *

47. 파이(π)란 무엇인가

원의 둘레가 c, 지름이 d일 때, c/d는 언제나 파이이다.

덧붙여서 타우(τ)는 2π를 의미한다.

48. 각도와 라디안

Math.Deg2Rad(a); // 각도에서 라디안으로
// pi/180 * a

Math.Rad2Deg(a); // 라디안에서 각도로
// 180/pi * a

49. 삼각형

유클리드 공간에서의 삼각형의 내각의 합은 언제나 180도이다.

정삼각형, 이등변삼각형, 부등변삼각형, 직각삼각형이 있다.

직각삼각형은 이등변삼각형, 부등변삼각형 둘 다 될수 있다.

50. 피타고라스의 정리

이등변 삼각형에서의 빗변의 길이는 a√2이다. 피타고라스의 정리는 삼각형의 내각을 구하는데에는 용이하지 않다.

51. 사인, 코사인, 탄젠트 1부

반지름이 1인 단위원에서는 x=cos, y=sin이 된다.

탄젠트는 원과 접선하여 x축과 만나는 직선이다.

52. 사인, 코사인, 탄젠트 2부

30도, 60도 역시 자주 사용된다. 정삼각형의 내각이 60도이기 때문이다. 그려진 직각 삼각형은 정삼각형의 절반이 된다.

30도, 60도는 서로 역수 관계이다.

1사분면을 제외한 나머지 사분면마다 양수를 가지는 함수가 다르다.

53. SOH, CAH, TOA

대변과 인접변은 세타를 기준으로 정해진다.

추가로 세타를 구할때는 양변에 역함수를 곱해서 구한다.

삼각함수를 쓸 수 있는 예시 상황은 공격 유효 범위 계산이다.

40. 완전제곱식 1

41. 완전제곱식 2

꼭짓점의 좌표가 제공되지 않는 경우, 완전제곱식으로 찾으면 된다.

42. 인수분해를 이용한 2차 방정식 풀이

2와 6은 어떻게 구했는가? b의 평균값인 4로 식을 하나 세우면 된다.

a가 1이 아닌경우에는 이렇게 안풀릴텐데, 근의 공식으로 두 근을 찾으면 된다.

43. 접점이 2개 이하인 포물선

u²=0이라면 축과의 접점이 1개, u²>0이라면 축과의 접점이 2개, u²<0이라면 축과의 접점이 없다.

위와 같은 2차 방정식이 있을 때,

 

완전제곱식은 바로 꼭짓점의 좌표가 된다.