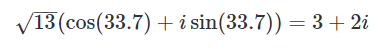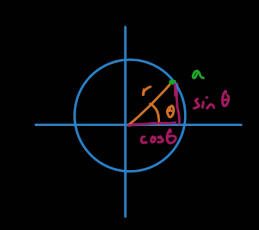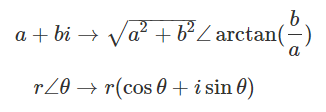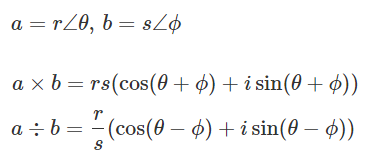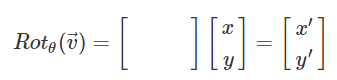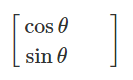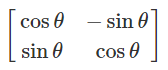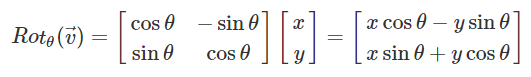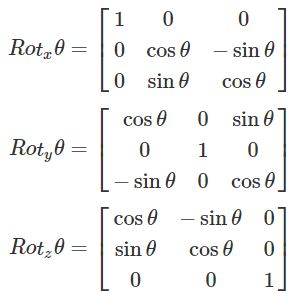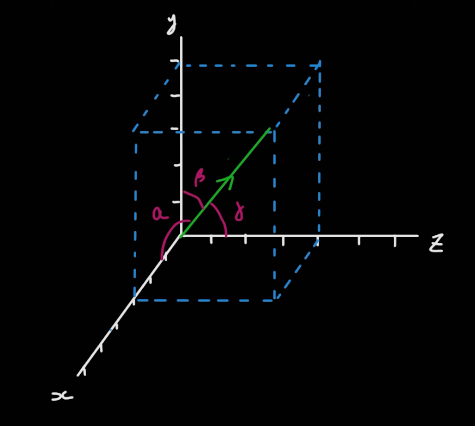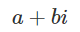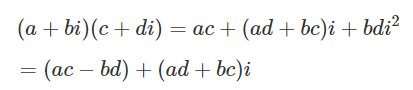91. 사원수란 무엇인가

위와 같은 형태를 가진다. 복소수를 확장시켜서 나온 개념이다.

92. 사원수 곱셈 1부

실수와 복소수에서의 곱셈은 교환법칙이 성립하지만 사원수에서는 곱셈의 교환법칙이 성립하지 않는다.

사원수끼리의 곱셈은 포일 메서드와 같이 각 요소마다 총 16번 곱해주면 된다.

전개된 식을 위의 i, j, k 관계로 다시 정리하면 약간 더 단순화 된다.

93. 사원수 곱셈 2부

전개식을 마저 정리하면 실수곱, 내적, 외적으로 깔끔하게 정리된다.

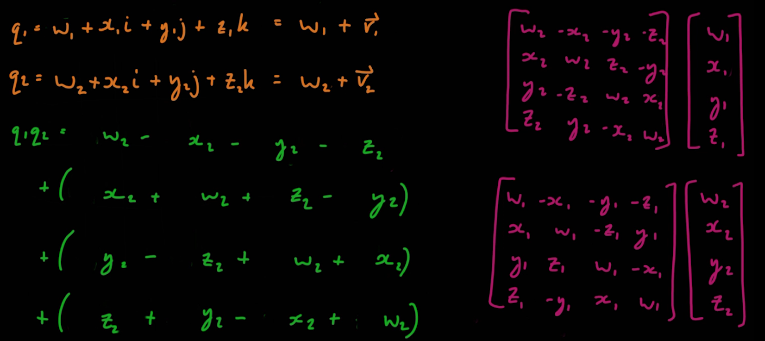
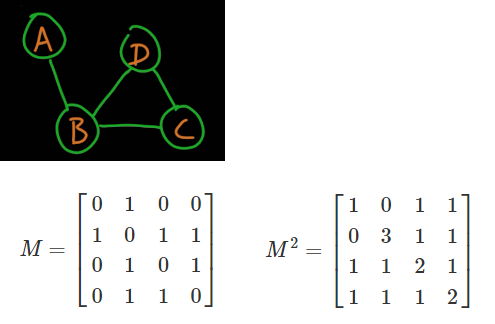
행렬로 더 깔끔하게 정리할수도 있다. 4x1행렬에 어떤걸 놓느냐에 따라 일부 부호가 달라진다.

94. 사원수 회전 1부

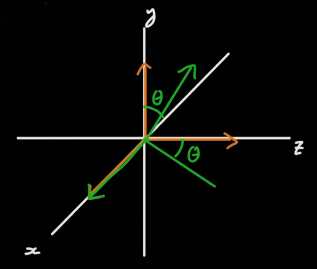
사원수의 곱으로 발생되는 회전은 일종의 4차원 회전이다. 하지만 4차원은 시각적으로 표현하기가 매우 어렵기때문에 jk평면에서의 회전은 볼 수 있지만 i의 복소평면에서의 회전은 시각적으로 회전으로 보이지 않고 i, -i 사이에서 값이 생겼다가 사라졌다 한다.

위의 그림은 i축을 기준으로 회전한것을 표현한것인데, 허수축에서 jk평면 회전과 i의 복소평면에서의 회전 총 2번이 이루어진다고 보면 된다.

시각적으로 상상하기가 매우 어려운게 맞다.

3차원 물체가 z축 앞뒤로 움직이는것을 2차원 xy평면에서 바라본다고 하면 평면에서 사라졌다가 생겼다가 하기 때문이다. (2차원 평면과 닿아있는 단면만 볼 수 있다.)

95. 사원수 회전 2부

어떤 사원수 q에 입력벡터 v를 곱하면(qv) 3차원에서의 회전과 4차원에서의 회전이 이루어진다.

어떤 입력벡터 v에 켤레사원수 q*를 곱하면(vq*) 3차원에서의 회전과 4차원에서의 역방향 회전이 이루어진다.

이 둘을 결합하면 qvq*가 되고 같은 방향으로의 3차원 회전이 두번 이루어지고 4차원에서의 회전이 상쇄되어 2번의 3차원 회전만 남게된다.

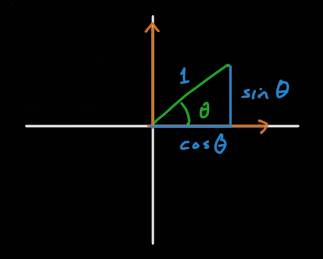
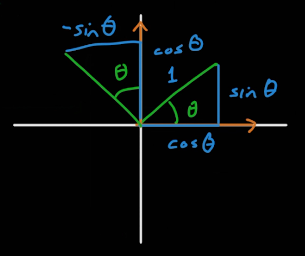
잠시 2차원에서의 회전을 짚어보고 가자.

v를 θ만큼 회전시킨게 v'이라고 했을 때, 공식은 위와 같다. 이 공식을 사원수로 확장시켜보자.

복소평면에서의 i축을 실수, ijk공간을 하나의 축으로써 본다. ijk공간은 실제로 3차원 공간이지만 표현상 2차원으로밖에 되지 않는다.

복소평면에서 실수축과 직교하는 i축이 있는것처럼 ijk공간에 존재하는 벡터 u의 축은 실수축과 직교한다. 또한 벡터 u는 회전축을 나타낸다. 벡터 u를 전개한 사원수 q는 다음과 같다.

앞서 qvq*는 3차원 회전이 두번 이루어지고 4차원 회전이 상쇄되었다고 했다. 하지만 우리가 회전하고자 하는 각은 θ이지 2θ가 아니다. 그래서 θ가 아닌 θ/2를 사용하게 된다.

최종적으로 위의 식이 완성된다.

사원수의 곱은 어떻게 작동하는지 정확히 이해하고 난 뒤에 특별히 수정해야 할 일이 발생하지 않는 한 만들어진 코드를 수정하지 않는것이 좋다.

마지막으로, 사원수의 곱에 의한 회전이 2배로 이루어지는것 때문에 180도 이상의 회전을 나타낼 수 없다.

87. 극좌표

직교형식으로 된 복소수 a가 3+2i라고 했을때 극형식으로 바꾸면 √13∠33.7이 나오게 된다.

극형식으로 표현된 √13∠33.7을 단위원의 삼각함수에서 유도된 공식에 극형식의 값을 대입하면 다시 직교형식으로 바꿀 수 있다.

복소수의 곱셈 결과는 두 복소수의 크기를 곱한것과 두 복소수의 각을 더한것과 같다고 했었다.

이를 이용하여 일반식으로 정리할 수 있다.

일반적으로 덧셈과 뺄셈은 직교형식으로 동류항끼리 계산하는게 더 쉽지만 곱셈과 나눗셈은 극형식으로 계산하는게 훨씬 쉽다.

그래서 두가지 방식을 다 알아야한다.

88. 회전 행렬

2차원 벡터 v=(x, y)를 θ만큼 회전시킨 결과가 v'=(x', y')라고 했을 때, 행렬로 표현하면 위와 같을 것이다.

열벡터에 곱해서 회전이 이루어지는 행렬을 찾는것이 이번 목표이다.

우선은 2x2 단위행렬을 떠올리자. 여기서부터 회전 행렬을 만들어 나갈 것이다.

단위행렬은 열벡터 2개로 나누어서 생각할 수 있다.

이 단위행렬에 의해 만들어진 벡터(1,0)로 원을 그리면 단위원이 될 것이고 θ만큼 회전시키면 인접변은 cosθ, 대변은 sinθ가 된다.

열벡터 한쪽이 채워졌다.

이번에는 다른 열벡터(0,1)를 θ만큼 회전시킬 차례이다.

두 벡터 모두 크기가 1이기때문에 길이 역시 똑같을 것이다. 하지만 sinθ가 2사분면으로 넘어왔기 때문에 음수가 된다.

단위행렬로 시작해서 회전행렬을 모두 구했다.

점 하나에 대한 회전이기 때문에 여러 정점으로 이루어진 오브젝트라면 각 정점마다 연산을 해야한다.

89. 오일러 행렬

2차원에서의 회전 행렬을 알아봤으니 이제는 3차원에서의 회전 행렬을 알아볼 차례이다.

마찬가지로 3x3 단위행렬에서 시작한다. 그리고 각 축을 기준으로 회전시킨다.

x축을 기준으로 (1,0,0)을 아무리 회전시켜봐야 그대로이고 나머지 축은 θ만큼 시계방향으로 회전하게 된다.

기준 축으로는 값의 변화가 없기때문에 사실상 2개의 축, 즉 2차원에서의 회전이라고 보면 되기 때문에 나머지 축에 대해서는 2차원에서의 회전을 적용하면 된다.

그렇게 구해진 각 축별 회전행렬은 위와 같다.

보통 피치-롤-요 순으로 연산한다.

그런데 이런 오일러각 회전에는 짐벌락이라는 아주 중대한 문제가 존재한다.

90. 짐벌락

중간축에 의해 외부와 내부 2개의 축이 일치하게 되면 축 하나가 상실된다.

자주 사용하는 축을 기준으로 연산 순서를 바꿔서 짐벌락 발생을 최소화시킬수 있지만 짐벌락을 막는것은 불가능하다.

83. 벡터의 방향

벡터의 방향은 한 점에서 다른 점을 빼면 구할 수 있다. 하지만 방향이 아닌 각도로 알고 싶다면?

2차원 벡터라면 단순하다. x, y좌표가 그대로 인접변, 대변의 길이가 되기 때문에 arctan(y/x)를 해주면 쉽게 구할 수 있다.

하지만 3차원 벡터는 조금 더 까다롭다.

삼각함수는 3개의 축에 적용할 수 없기 때문에 2개의 축에 대한 삼각함수를 구해서 계산을 한다.

먼저 본래의 벡터 v를 xz축에 투영시킨 2차원 벡터 v'로 만들고 그 각 Φ을 구한다. 그리고 v와 v'를 이으면 v'에 직교하는 법선벡터가 만들어지며, v와 v'의 끼인각을 알아낼 수 있다.

y축과 v'는 서로 직교하기 때문에 90-끼인각을 계산하면 최종적으로 θ를 알아낼 수 있다.

근데 이 방법은 복잡하고 더 쉬운 방법이 있다.

먼저 각 축 x, y, z와 벡터 사이의 각을 각각 α, β, γ라고 하자. 그리고 벡터의 크기를 구하면 해당 벡터의 크기는 각 축에 공통적인 빗변의 크기가 될 것이고 각 축은 인접변이 될 것이다.

빗변과 인접변? cosθ이다.

벡터의 방향을 이런식으로 구하면 회전을 할 때 매우 유용하다.

84. 허수

기존의 실수체계는 1차원이었다면 허수는 2차원 평면으로 확장된다.

0에서 1까지의 거리와 0에서 i까지의 거리는 같다.

지수가 커질수록 기하급수적으로 커지거나 작아지는 실수와는 다르게 허수는 90º씩 계속 순환할뿐이다.

85. 복소수

실수부와 허수부로 이루어진 수이다.

그럼 이 복소수를 대체 왜 쓰는걸까?

그 이유는 회전 계산에 매우 유용하기 때문이다.

복소수의 연산은 기본적으로 벡터와 동일하다.

86. 복소평면

우선 복소수의 곱셈부터 알아보자.

단순히 전개식으로 풀어도 동일한 결과가 나온다. 단지 i의 제곱이 -1이라는 점을 이용하여 일반식으로 만든것일 뿐이다.

복소수의 곱셈의 결과를 그래프로 그려보면 꽤 재밌는 결과가 나온다.

각 복소수로 그려진 직각삼각형의 각도를 더한것과 같은 결과가 나오게 된다.

즉, 두개의 복소수를 곱하면 그 결과는 복소평면에서 회전을 한다. 또한 결과의 크기는 두 선의 크기를 곱한 값과 같다.

복소수의 표현 방식은 직교형식, 극형식 2가지로 구분할 수 있다.

78. 단위행렬

어느 행렬에 곱해도 언제나 1을 곱한것과 같다. 단위행렬은 반드시 정방행렬 이어야 한다.

79. 행렬식

행렬식의 값이 0이 아니면 역행렬이 존재한다.

4x4행렬은 라플라스 전개식을 총 4번 수행하면된다.

80. 역행렬

3x3행렬은 조금 복잡하다.

1) 소행렬식을 먼저 구하고

2) 여인자 행렬로 변환하고

3) 여인자 행렬을 전치시킨뒤

4) 행렬식의 역수를 곱한다

최종적으로 위와 같은 식이 완성된다.

수기로 계산하게되면 과정이 복잡하고 많기때문에 실수에 유의해야한다.

보통 게임 엔진이나 라이브러리는 벡터와 마찬가지로 행렬 연산에 대한 함수를 제공해준다.

74. 행렬이란 무엇인가

75. 행렬의 합 및 스칼라 곱셈

76. 인접행렬

그래프 탐색으로 길을 찾을때 사용될 수 있다.

77. 행렬의 곱셈

위에서 작성한 그래프의 인접행렬을 제곱하면 두번 이동해서 도착할 수 있는 경로의 갯수가 나오게된다.

세제곱을 하면 세번 이동해서 도착할 수 있는 경로의 갯수가 나오게된다.

행렬의 곱셈은 내적과 같다.