54. 사인 법칙

위와 같은 삼각형이 주어졌을 때,
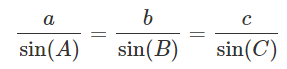
위의 식이 성립한다.
예시 문제를 하나 풀어보자.

각 2개와 변 1개를 알고 있고 변이 두 각 사이에 있지 않을 때, 나머지 값들을 구할 수 있다. (AAS)

B가 포탑이고 최대사거리가 7이라고 했을 때, 5.72 <= 7이므로 공격이 가능하다.
반대로 각 1개와 변 2개(밑변 제외)를 알고 있어도 값을 구할 수 있다. (SSA)


sin(B)가 아닌 B를 구하는게 목적이기 때문에 0.384에 역함수를 취해서 B의 값을 구한다.
단, 주의할점이 있다. 각도에 대한 사인 값만 알고 다른 정보가 없을 경우 1사분면과 2사분면의 사인값은 둘다 양수이기 때문에 해가 2개이다. (22.58º 또는 157.42º)
밑변의 길이가 다른 삼각형이 여러개 존재할 수 있는 것이다.
찾아본 바로는 사인 법칙이 적용되는 예는 아래와 같다
◾ 한 변의 길이와 양 끝각의 크기를 알 때
◾ 두 변의 길이와 그 끼인각이 아닌 각의 크기를 알 때
55. 코사인 법칙
AAS, SSA의 경우는 사인 법칙으로 구할 수 있지만 SAS(변,각,변), SSS(변3개)는 코사인 법칙으로 구할 수 있다.


이런 경우가 주어졌다면 위의 식에 그대로 대입해서 구하면 된다.

이번에는 변의 길이만 주어진 경우를 보자.

A를 구하는 경우에는 cos(A)에 역함수를 취해주면 된다.
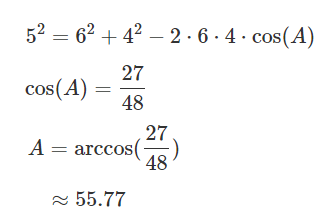
나머지 두 각은 B에대해 한번 더 같은 과정을 수행하고 180-A-B로 간단히 구할 수 있다.
56. 사인, 코사인 법칙에 대한 설명
■ 사인 법칙 유도과정


C도 마찬가지로 A에서 수선의 발을 내려서 구하면 된다.
예각 삼각형이 아닌 둔각 삼각형이라면 삼각형 외부에 또 다른 삼각형을 그려서 직각 삼각형을 만든 다음 구하게 된다.
■ 코사인 법칙 유도과정 : https://erikanes.tistory.com/147
조금 더 단순하게 구하기
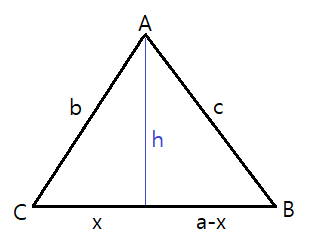

a, b 역시 동일하게 수선의 발을 내려서 직각삼각형을 만들고 식을 만들면 된다.
57. 삼각형 문제의 해법

◾ 각도만 3개 주어졌을 때(AAA) : 각 변의 길이를 구할 수 없다.
◾ 직각 삼각형이고 빗변을 구해야 하는 경우(SSS) : 피타고라스의 정리 이용
◾ 직각 삼각형이고 빗변이 아닌 변을 구해야 하는 경우 : SOH, CAH, TOA
◾ AAS, SSA, ASA : 사인 법칙 이용. 답이 2개일수도 있으니 주의해야한다
◾ SAS, SSS : 코사인 법칙 이용
59. 사인파의 조작
◾ 진폭(amplitude) : 사인 파동의 높낮이를 조절한다.
◾ 주파수(frequency) : 사인 파동의 간격을 조절한다.

60. 파장의 합성
* 추후 사진 첨부 *
'이론 > 게임수학' 카테고리의 다른 글
| [게임수학] 벡터와 행렬 (2) (0) | 2023.01.11 |
|---|---|
| [게임수학] 벡터와 행렬 (1) (0) | 2023.01.10 |
| [게임수학] 각도와 원에 대한 소개 (1) (0) | 2023.01.09 |
| [게임수학] 대수학과 방정식 (3) (0) | 2023.01.09 |
| [게임수학] 대수학과 방정식 (2) (0) | 2023.01.09 |
