63. 벡터 읽고 쓰기
크기와 방향을 가지고 있다. 크기가 1인 경우 단위 벡터이다.
64. 크기와 크기의 제곱

원점에서 시작하는 벡터 OA의 크기는 직각삼각형의 빗변으로도 볼수 있기 때문에 피타고라스의 정리로 구할 수 있다.

원점에서 시작하지 않는 벡터는 직선의 방정식에서 기울기를 구하던 것처럼 변화량으로 계산하면 된다.
3차원 벡터의 크기 계산은 별 다를것 없이 z축만 추가해주면 된다.

다만 유의해야 할 점은 제곱근 연산은 비용이 꽤 큰 연산이기 때문에 크기를 구할때마다 매번 제곱근을 계산하기에는 부담스럽다. 그래서 대신 크기에 제곱을 취해서 제곱근 연산을 피한다.

어떤 값(ex:적의 공격범위)과 비교해야 할 때, 양변에 제곱을 취해서 비교하는것이 연산량이 훨씬 적다.
두 벡터 사이의 거리를 계산해야 할 때는 제곱근 연산을 피하는게 좋고 유저에게 정보를 보여줘야 할때는 정확한 정보가 필요하기 때문에 제곱근 연산을 할 수밖에 없을 것이다.
대부분의 게임 엔진은 벡터의 크기를 반환하는 함수를 위의 두 종류로 제공한다.
66. 벡터의 덧셈

활용 예)
◾ 플레이어와 카메라 간의 위치 차이 측정
◾ 바람에 밀리는 오브젝트
교환 법칙이 성립된다.
67. 스칼라 곱셈

각 요소에 스칼라값을 곱해주면 된다.
68. 벡터의 정규화
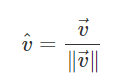
벡터의 크기가 0이라면 오류가 발생하기 때문에 주의해야한다.
69. 영벡터
프로그래밍을 하다보면 영벡터를 꽤 자주 만나게 되고 유용하게 사용하는 경우가 있다.
직전에도 언급했듯이 영벡터의 정규화를 시도하는 것에 주의해야한다.
'이론 > 게임수학' 카테고리의 다른 글
| [게임수학] 벡터와 행렬 (3) (0) | 2023.01.11 |
|---|---|
| [게임수학] 벡터와 행렬 (2) (0) | 2023.01.11 |
| [게임수학] 각도와 원에 대한 소개 (2) (0) | 2023.01.10 |
| [게임수학] 각도와 원에 대한 소개 (1) (0) | 2023.01.09 |
| [게임수학] 대수학과 방정식 (3) (0) | 2023.01.09 |
