 제1코사인법칙
제1코사인법칙
더보기
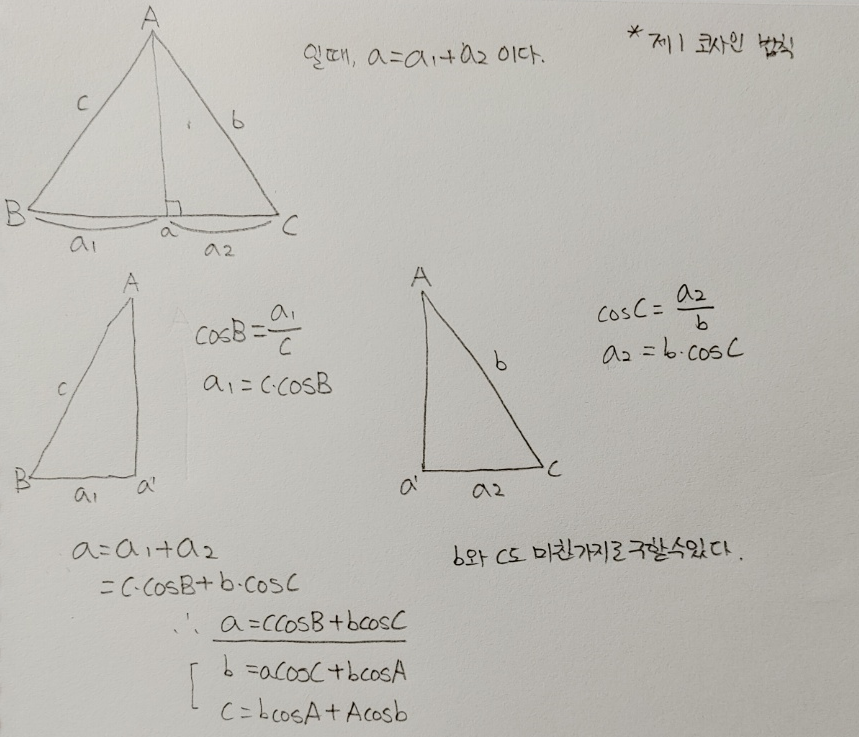 제1코사인법칙 식 유도과정
제1코사인법칙 식 유도과정
 제2코사인법칙
제2코사인법칙
더보기
 제2코사인법칙 식 유도과정
제2코사인법칙 식 유도과정
내적
3차원 벡터 A=(ax, ay, az), B=(bx, by, bz)가 주어졌을 때,
A·B = (axbx + ayby + azbz) = |A||B|cosθ 로 계산할 수 있으며 결과는 스칼라값으로 나온다.
|A||B|cosθ는 제2코사인법칙을 사용하면 구할 수 있는 동일한 식이다.
교환법칙, 분배법칙, 스칼라곱에 대한 결합법칙이 성립한다.
더보기
 벡터의 내적 식 유도과정
벡터의 내적 식 유도과정
■ 두 벡터간의 직교성을 판별하는데 사용할 수 있다.
A·B=0 이라면 두 벡터는 직교(90°)한다.
A·B=1 이라면 두 벡터는 평행(0°)한다. 같은 방향을 바라본다는 뜻이다.
A·B=-1 이라면 두 벡터는 평행(180°)한다. 서로 다른 방향을 바라본다는 뜻이다.
앞뒤판별에 사용할 수 있다.
■ 두 벡터간의 투영 길이를 구하는데 사용할 수 있다.
외적
외적은 3차원 벡터에 대해서만 사용할 수 있다.
3차원 벡터 3차원 벡터 A=(ax, ay, az), B=(bx, by, bz)가 주어졌을 때,
A×B = (aybz-azby, azbx-axbz, axby-aybx) 로 계산할 수 있다.
교환법칙과 결합법칙이 성립하지 않는다. (교환하는 경우 부호가 반대로 나온다.)
벡터 삼중곱
A×(B×C) = (A·C)·B - (A·B)·C (사원수 식 유도에서 사용됨)
더보기
 벡터의 외적 식 유도과정
벡터의 외적 식 유도과정
두 벡터를 외적하면 두 벡터에 모두 직교하는 새로운 벡터가 생성된다.








