83. 벡터의 방향
벡터의 방향은 한 점에서 다른 점을 빼면 구할 수 있다. 하지만 방향이 아닌 각도로 알고 싶다면?

2차원 벡터라면 단순하다. x, y좌표가 그대로 인접변, 대변의 길이가 되기 때문에 arctan(y/x)를 해주면 쉽게 구할 수 있다.
하지만 3차원 벡터는 조금 더 까다롭다.
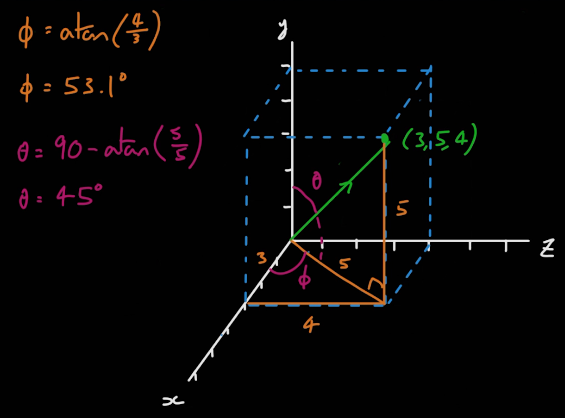
삼각함수는 3개의 축에 적용할 수 없기 때문에 2개의 축에 대한 삼각함수를 구해서 계산을 한다.
먼저 본래의 벡터 v를 xz축에 투영시킨 2차원 벡터 v'로 만들고 그 각 Φ을 구한다. 그리고 v와 v'를 이으면 v'에 직교하는 법선벡터가 만들어지며, v와 v'의 끼인각을 알아낼 수 있다.
y축과 v'는 서로 직교하기 때문에 90-끼인각을 계산하면 최종적으로 θ를 알아낼 수 있다.
근데 이 방법은 복잡하고 더 쉬운 방법이 있다.
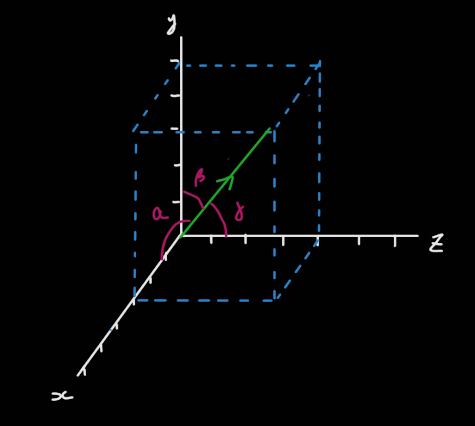
먼저 각 축 x, y, z와 벡터 사이의 각을 각각 α, β, γ라고 하자. 그리고 벡터의 크기를 구하면 해당 벡터의 크기는 각 축에 공통적인 빗변의 크기가 될 것이고 각 축은 인접변이 될 것이다.
빗변과 인접변? cosθ이다.

벡터의 방향을 이런식으로 구하면 회전을 할 때 매우 유용하다.
84. 허수
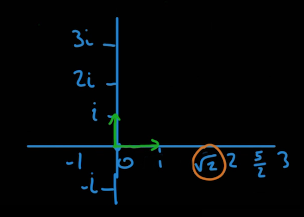
기존의 실수체계는 1차원이었다면 허수는 2차원 평면으로 확장된다.
0에서 1까지의 거리와 0에서 i까지의 거리는 같다.

지수가 커질수록 기하급수적으로 커지거나 작아지는 실수와는 다르게 허수는 90º씩 계속 순환할뿐이다.
85. 복소수
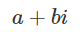
실수부와 허수부로 이루어진 수이다.
그럼 이 복소수를 대체 왜 쓰는걸까?
그 이유는 회전 계산에 매우 유용하기 때문이다.
복소수의 연산은 기본적으로 벡터와 동일하다.
86. 복소평면
우선 복소수의 곱셈부터 알아보자.

단순히 전개식으로 풀어도 동일한 결과가 나온다. 단지 i의 제곱이 -1이라는 점을 이용하여 일반식으로 만든것일 뿐이다.
복소수의 곱셈의 결과를 그래프로 그려보면 꽤 재밌는 결과가 나온다.

각 복소수로 그려진 직각삼각형의 각도를 더한것과 같은 결과가 나오게 된다.
즉, 두개의 복소수를 곱하면 그 결과는 복소평면에서 회전을 한다. 또한 결과의 크기는 두 선의 크기를 곱한 값과 같다.

복소수의 표현 방식은 직교형식, 극형식 2가지로 구분할 수 있다.
'이론 > 게임수학' 카테고리의 다른 글
| [게임수학] 회전과 보간 (3) (0) | 2023.01.13 |
|---|---|
| [게임수학] 회전과 보간 (2) (0) | 2023.01.12 |
| [게임수학] 벡터와 행렬 (4) (0) | 2023.01.11 |
| [게임수학] 벡터와 행렬 (3) (0) | 2023.01.11 |
| [게임수학] 벡터와 행렬 (2) (0) | 2023.01.11 |
